Eulero trova una dimostrazione

Il secondo articolo, di cui qui ci sono la versione latina originale e una traduzione inglese, si intitola DEMONSTRATIO NONNVLLARUM INSIGNIVM PROPRIETATVM, QVIBVS SOLIDA HEDRIS PLANIS INCLVSA SVNT PRAEDITA , (DIMOSTRAZIONE DI ALCUNE NOTEVOLI PROPRIETA', DI CUI SONO DOTATI I SOLIDI RACCHIUSI DA FACCE PIANE).

Inizia facendo un po' la storia del suo interesse per i poliedri  e racconta come 'non sine summa admiratione' abbia scoperto nuove proprietà, per alcune delle quali però  non è riuscito a trovare una dimostrazione, neppure chiedendo l'aiuto di 'versatissimi' amici, tanto da arrivare al punto di pensare che facessero parte di quelle verità che non ci è concesso di dimostrare. Le due verità a cui si riferisce, e che qui riporta, sono quelle menzionate nel precedente articolo e specifica che sono strettamente dipendenti, perché ognuna implica l'altra, e quindi basterebbe dimostrare una delle due.
Alla fine però è finalmente arrivato a una dimostrazione, sulla falsariga di quella usata in geometria piana per trovare la somma degli angoli di un poligono. Come in geometria piana tagliando via gli angoli di un poligono ci si riduce alla fine ad un triangolo, così osservò che in un poliedro si possono tagliare via in successione gli angoli solidi e alla fine ci si riduce ad una piramide triangolare, e quindi si rese conto che dalle proprietà di questa figura semplicissima si potrebbe risalire alle proprietà di un poliedro qualsiasi.
Un primo modo di tagliuzzare un poliedro potrebbe essere di prendere un punto interno e collegarlo con tutti i vertici, ottenendo una suddivisione in piramidi, ognuna delle quali potrebbe a sua volta essere suddivisa in piramidi a base triangolare: questa via però si rivela infruttuosa.
Il modo buono è quello che espone nel resto dell'articolo, iniziando con una analogia tratta dalla geometria piana.

In geometria piana ci sono varie dimostrazioni per calcolare la somma degli angoli interni di un poligono; quella che qui presenta Eulero non è la più semplice, però ugualmente interessante. Sia dunque dato un poligono (convesso) di L lati e sia R il numero di angoli retti uguale alla somma di tutti gli angoli interni. Se si taglia via un vertice e i due lati corrispondenti mediante un taglio che passa per i due vertici adiacenti, il numero di lati del poligono rimanente diminuisce di 1 mentre la somma degli angoli diminuisce di 2 retti (perché si toglie un triangolo); dopo un certo numero n di tagli si rimarrà con un unico triangolo, con 3 lati e 2 retti come somma degli angoli; quindi in seguito ai tagli risulta L-n=3 e R-2n=2, da cui 2L-R=4 e quindi R=2L-4 .
Volendo ripetere la stessa strategia su un poliedro, le cose si complicano un po' e infatti Eulero impiega una quindicina di pagine per tenere conto delle varie situazioni che possono presentarsi. Qui cerco di riassumere i passaggi fondamentali.

Sia dato un poliedro, che si suppone convesso anche se Eulero non lo dice, con V vertici, F facce e S spigoli (Eulero usa le lettere S, H, A come già detto). L'idea è di tagliare via un vertice con gli spigoli relativi e vedere che cosa succede al poliedro rimanente. Se dal vertice partono solo 3 spigoli la cosa è abbastanza semplice, ma se sono di più nascono delle complicazioni. Se nel vertice O arrivano n spigoli, raggruppando terne di spigoli consecutivi, si possono individuare n-2 piramidi con base triangolare e vertice O, rimuovendo le quali scompare il vertice O con gli n spigoli

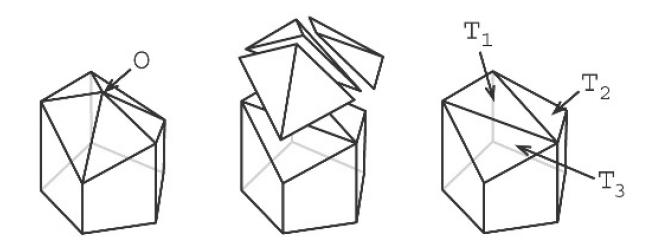Nell'esempio qui a sinistra n vale 5 e vengono rimossi 3 tetraedri: nascono 3 nuove facce e 2 nuovi spigoli, mentre scompaiono 5 spigoli e 5 facce. Una prima complicazione potrebbe sorgere se T₁ e T₂ o T₁ e T₃ fossero complanari, perché cambierebbe il conteggio delle nuove facce e dei nuovi spigoli. Supponendo che non ci siano coppie contigue di nuove facce complanari, in generale se da O partono n spigoli, scompaiono n spigoli e ne nascono n-3 di nuovi e scompaiono n facce mentre ne nascono n-2: perciò il nuovo poliedro ha V-1 vertici, F-2 facce e S-3 spigoli. In questo esempio tutte le facce rimosse sono triangoli, ma se alcune avessero avuto più lati il calcolo non sarebbe più valido, e questo indica un'altra possibile situazione da studiare.

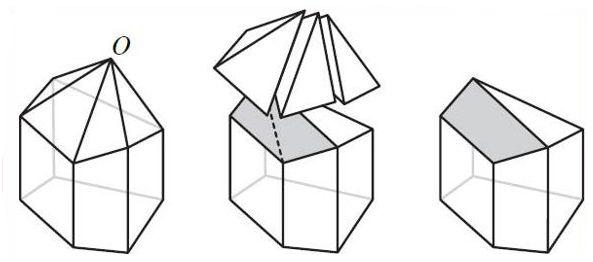In questo esempio ci sono due nuove facce contigue complanari che in realtà formano una unica faccia non triangolare. Per ogni coppia di nuove facce contigue complanari bisogna togliere 1 sia dal conteggio delle nuove facce che dei nuovi spigoli: quindi se ci sono k di tali coppie il nuovo poliedro ha V-1 vertici, F-2-k facce e S-3-k spigoli.

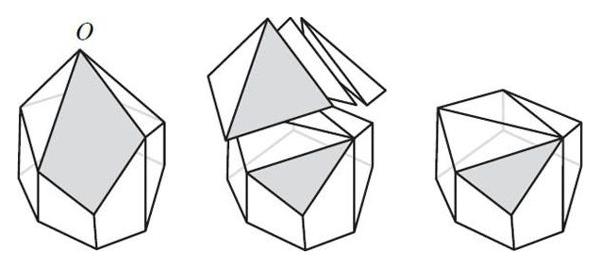In questo esempio c'è una faccia non triangolare, che va tagliata per poter asportare un tetraedro: come risultato compare un nuovo spigolo e una nuova faccia: se ci sono t facce non triangolari il conteggio precedente si modifica in questo modo: V-1 vertici, F-2-k+t facce e S-3-k+t spigoli.

La cosa notevole è che per il nuovo poliedro, indipendentemente da k e t, la quantità V'+F'-S'=(V-1)+(F-2-k+t)-(S-3-k+t)=V+F-S non cambia valore e quindi basta calcolare questo valore: siccome alla fine ci si riduce sempre ad un tetraedro che ha V=4 F=4 S=6 e quindi V+F-S=2, questo vale per tutti i poliedri.

 In realtà Eulero la fa un po' più lunga e si sofferma sul calcolo di S-F che ad ogni vertice rimosso si riduce di 1 e nel frattempo nota anche che questa quantità dà la somma degli angoli delle facce (in angoli giri), il che alla fine lo conduce, mediante la relazione V-2=S-F, alla conclusione, di cui è parecchio soddisfatto, che tale somma vale V-2 e dipende solo dal numero di vertici.

In seguito Eulero non tornò più sull'argomento, e probabilmente non si rese conto di aver dato uno dei calci d'inizio al nuovo filone della topologia (l'altro l'aveva dato ancora prima con lo studio dei grafi), e quindi la storia non finisce qui.