Critiche e nuove dimostrazioni

Nella dimostrazione di Eulero si notarono presto dei punti non tanto rigorosi, in quanto egli non era stato molto chiaro sul processo di rimozione delle piramidi triangolari: siccome per ogni vertice le piramidi si possono scegliere in vari modi, e questo lo dice, non avverte però che alcune scelte possono portare a situazioni di stallo.

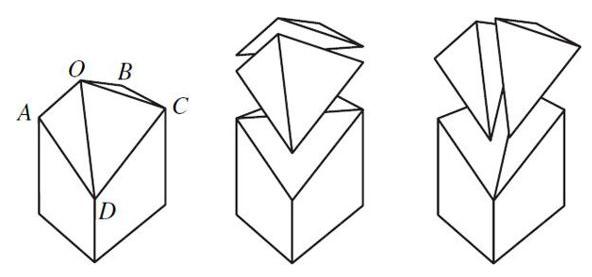Come esempio, può succedere che si arrivi ad un poliedro non convesso, come si vede nella figura qui a fianco. Però si vede anche che esiste una scelta che evita il problema.

La questione è se esiste sempre una scelta buona.

Tra le scelte cattive alcune possono portare anche a poliedri degeneri come quelli costituiti da due poliedri collegati per uno spigolo o per un vertice, per i quali la formula non vale più.

Un altro bel problema è stabilire per quali poliedri vale la formula.

Con il passare del tempo si precisarono le definizioni di poliedro e in particolare di poliedro convesso, e nel 1794 comparve una prima dimostrazione esente dalle critiche dell'algoritmo di Eulero: si trova negli Eléments de Géométrie di Legendre, un testo molto fortunato che segnò una pietra miliare nella didattica della geometria. Il libro VI è dedicato allo studio dei poliedri, ma quando vi ho cercato la nostra formula con sorpresa non ne ho trovato traccia. E allora? Allora bisogna scorrere il libro VII (qui un breve estratto) che si intitola Sphère (Sfera) , perché la dimostrazione si basa sulle proprietà dei triangoli sferici. L'idea originale è questa: dato un poliedro convesso, prendiamo un punto O al suo interno e disegniamo una sfera di centro O che contenga tutto il poliedro; poi proiettiamo da O sulla sfera tutti i vertici e gli spigoli; in questo modo la superficie sferica resta divisa in tanti poligoni geodetici (i lati sono archi di cerchi massimi) quante sono le facce. Già il greco Menelao sapeva che la somma degli angoli interni di un triangolo geodetico è sempre maggiore di due retti, e quindi vi è un eccesso rispetto alla stessa somma in un triangolo piano; fu all'inizio del XVII secolo che Harriot e Gerard indipendentemente quantificarono questo eccesso, legandolo all'area del triangolo: infatti se x,y,z sono le misure degli angoli del triangolo e r il raggio della sfera, l'area è \( A=r^2(x+y+z-\pi ) \) ; estendendo la formula ad un poligono con n lati viene \( A=r^2(somma\_angoli - (n-2) \pi )=r^2(somma\_angoli-n \pi +2 \pi ) \). Sommando le aree di tutti i poligoni viene \( 4 \pi r^2 \) , area della superficie sferica; calcolando la stessa somma usando i secondi membri della uguaglianza precedente vengono tre termini, moltiplicati per r² :  la somma di tutti gli angoli interni dei poligoni si ottiene considerando che la loro somma per ogni vertice è \(2 \pi \) e quindi in totale è \( 2 \pi V \); la somma di tutti i lati (n della formula) dei poligoni è il doppio degli spigoli perché ogni spigolo appartiene a due poligoni, e quindi fa \(2 \pi S \); poi c'è il 2 della formula che va moltiplicato per il numero di poligoni e quindi fa \( 2 \pi F \) : in totale viene \( 2 \pi V-2 \pi S+2 \pi F \). Uguagliando le aree e raccogliendo i fattori comuni risulta \( 4 \pi r^2=2 \pi r^2 (V-S+F) \) e semplificando \( 2=V-S+F \).

Geniale, ma non semplice da proporre ai nostri studenti, perché prima bisognerebbe dimostrare la formula dei triangoli sferici, cosa non impossibile ma non tanto usuale. La stessa osservazione si trova in un interessante articolo negli Annales de Mathématiques del 1813, in cui Gergonne riassume un lungo articolo di Lhuilier apparso su altra rivista: in esso Lhuiler propone una nuova dimostrazione, rispolverando la suddivisione del poliedro in piramidi aventi un vertice comune in un punto interno, che Eulero aveva scartato come infruttuosa, e mostra come la formula valga anche per poliedri non convessi, ma non per tutti: infatti ne analizza alcune tipologie per le quali non sussiste. A proposito di questa dimostrazione Gergonne conclude che per quanto sia più semplice di quella di Eulero ed esente da critiche, probabilmente è ancora migliore quella di Cauchy apparsa tempo prima.

Infatti Cauchy già nel 1811 aveva trovato una nuova dimostrazione innovativa e relativamente semplice, pubblicata nel 1813 nel Journal de l'école Polytechnique con il titolo Recherches  sur  les  polyèdres divisa in due parti: nell'articolo ci sono parecchi nuovi importanti risultati e anche la nuova famosa dimostrazione. L'idea innovativa consiste nell'appiattire sul piano il poliedro, conservando tutti i collegamenti tra i vertici ma non le distanze: un tipico esempio di trasformazione topologica. Le istruzioni per trasformare il poliedro in un grafo piano sono di questo tipo:

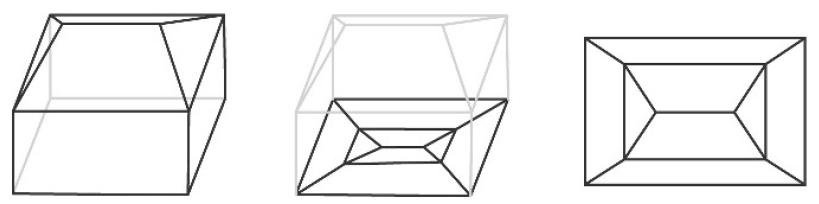"rimuovere una faccia del poliedro, poi trasportarvi tutti gli altri vertici, ottenendo così una figura piana formata da poligoni racchiusi dal contorno della faccia rimossa"
Il numero di poligoni è P=F-1, mentre gli spigoli, ora lati dei poligoni, sono sempre S e i vertici sempre V.

Ora sottoponiamo il grafo ottenuto ad alcune trasformazioni tenendo sotto occhio la quantità P+V-S

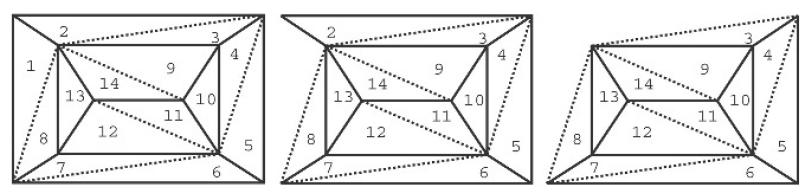Prima di tutto suddividiamo ogni poligono in triangoli: per ogni nuovo spigolo (tratteggiato) si crea anche un nuovo poligono, per cui la quantità P+V-S rimane invariata.
Poi rimuoviamo i triangoli partendo dall'esterno: ci sono due casi: 1) se il triangolo ha un solo spigolo a contatto con l'esterno, si rimuove questo spigolo e quindi anche il triangolo, perciò P+V-S non cambia; 2) se due spigoli sono a contatto con l'esterno, rimuoviamoli e così perdiamo un triangolo e un vertice, ma in ogni caso P+V-S non cambia. Alla fine rimarrà un unico triangolo per il quale P=1, V=3, S=3 e P+V-S=1 e questa relazione vale anche per il grafo iniziale; ricordando che P=F-1, viene F-1+V-S=1 e quindi F+V-S=2.

Questa dimostrazione è realmente semplice e credo abbordabile anche dai ragazzi di scuola media.

Dopo di questa arrivarono parecchie altre dimostrazioni (a questo indirizzo se ne trovano una ventina) .

Una carina fu proposta nel 1847 da von Staudt in Geometrie der Lage , in cui definisce prima due condizioni per la validità della formula: 1) da ogni vertice si possa raggiungere ogni altro muovendosi sugli spigoli, 2) ogni circuito semplice di spigoli divida il poliedro in due parti non comunicanti (per es. un poliedro a forma toroidale non va bene). A grandi linee la dimostrazione è così:

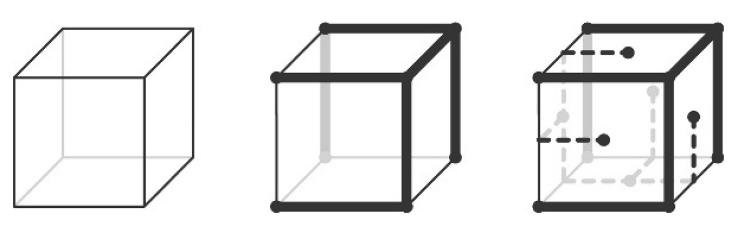
 Partendo da un vertice raggiungi tutti gli altri muovendoti sugli spigoli, snza mai chiudere un circuito: così hai percorso V-1 spigoli; ora parti da una faccia e, attraversando gli spigoli rimasti, raggiungi le altre facce: avrai attraversato F-1 spigoli. Quindi in totale gli spigoli sono (V-1)+(F-1)=V+F-2